A hypothesis test is a method for making rational decisions about the reality of effects.
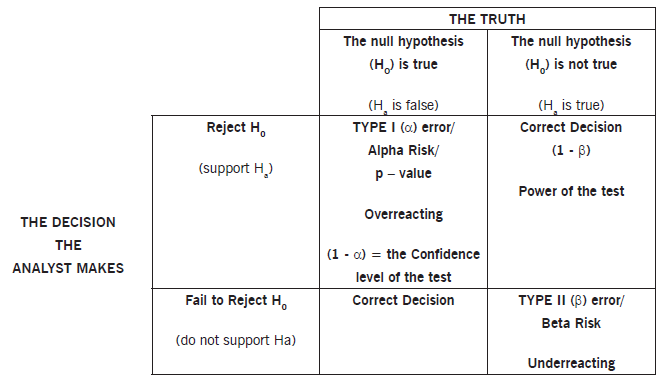
Use: Most decisions require choosing from one or more alternatives. The decision is based on incomplete information. A team might be considering using a different method which they believe will give them a better result. Their theory is that method A is going to be better than method B. The null hypothesis means that method A is no better or worse than method B. The alternative hypothesis is the opposite of the null hypothesis. The alternative hypothesis is that method A is better than method B. They will test to see if Method A gives them a better result. If it turns out that the two methods are equal to each other, the team will have failed to reject the null hypothesis. Meaning the two methods are essentially equal to each other. If, on the other hand, the team finds that method A is better than method B, the team has rejected the notion of equality (rejecting the null hypothesis).
The testing does come with some risk. If their conclusion is that they have rejected the null thinking that method A is better than method B, when in fact it really isn’t better, they have made a Type I error*. But, let’s say that their finding was that the two methods were the same, when in reality method A was better than B. If the team came to that conclusion, they will have made a Type II error**. Still confused? Visit our chi-square definition page which breaks this down into great detail.
*A Type I error is thinking that something is significantly different, when in fact it really isn’t.
** A Type II error thinking that something is not significantly different, when in fact it really is.