If a basketball coach measured the heights of the players to the nearest yard, all of the players would be two yards tall. The conclusion would be that there is no variation in the heights of basketball players. However, if the coach measured all of the players to the nearest foot, the players would either be 6 feet tall or 7 feet tall. Measure to the nearest inch, and the result would be a large variation in the heights of basketball players. How fine a measurement is sliced is referred to as Measurement Discrimination.
One way to visualize the amount of measurement discrimination is to look at the range portion of a control chart. It is points (dots) that you need to look at on the chart. You look for the number of strata (parallel layers) of the dots as they spread across the range chart. It is not the count of dots. Instead, it is a count of strata (parallel layers) of dots (you are looking for a minimum of six strata).
If given these ranges:
0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0
If all of the range values are at zero, there is only one strata – the zero line.
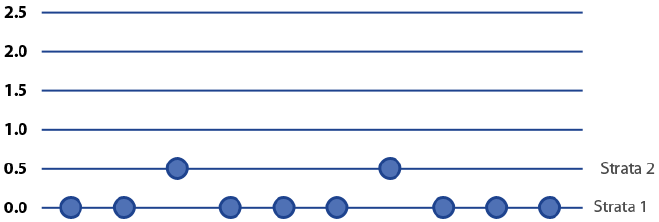
But if given these ranges:
0.0 0.5 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.5 0.0 0.0 0.5
Dots are found on the zero line and the 0.5 line. You would have two strata.
And if given these ranges:
0.0 0.5 0.0 0.0 1.0 0.0 1.0
1.0 0.0 0.0 0.5 0.0 0.0 0.5
You could find dots on the zero line, the 0.5 line, and the 1.0 line.
There would be three strata.
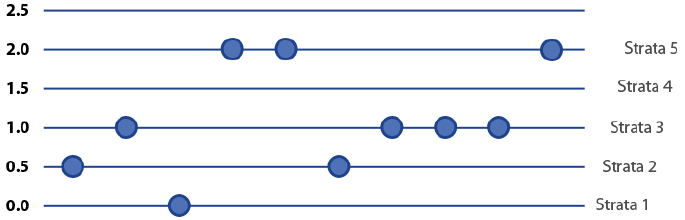
Finally, if you had these ranges:
0.5 0.0 2.0 1.0 1.0 2.0 0.0
1.0 2.0 0.5 1.0 2.0 0.0 1.0
You can see dots on the zero line, the 0.5 line, the 1.0 line, and the 2.0 line, but none of the dots on the 1.5 line. You still have five strata, even though you do not see any of the dots on the 1.5 line. There could be a dot on the 1.5 line – and there would eventually be – if we were to continue to gather data.
If you are using a control chart to determine measurement discrimination, the rule-of-thumb is to have at least six strata (units of measure) under the upper control limit of the range. Note: the zero line (strata) counts as one of the six desired units.
Why six points?
To understand why it is six points we are looking for, there needs to be an understanding of rounding. When measurements are rounded off too much, most of the information about dispersion is lost.
Example:
Individual values
72.7136
72.8248
72.1241
72.0136
72.6141
72.5098
72.3132
72.0144
If we had rounded (tens place), we would have gotten the following measurements:
70
70
70
70
70
70
70
70
We would have concluded: zero dispersion
If we had rounded (ones place), we would have gotten the following measurements:
73
73
72
72
73
73
72
72
We would have concluded: very little dispersion. Possible range values: 0, and the one’s place value. (Units = 2)
If we had rounded (tenths place), we would have gotten the following measurements:
72.7
72.8
72.1
72.0
72.6
72.5
72.3
72.0
We would have concluded: some dispersion. Possible range values: 0, and the one’s place value, and the tenth’s place holder. (Units = 3)
If we had rounded (hundredth place), we would have gotten the following measurements:
72.71
72.82
72.12
72.01
72.61
72.51
72.31
72.01
We would have concluded: more about dispersion. Possible range values: 0, and the one’s place value, the tenth’s place holder, and the hundredths place holder. (Units = 4)
Four is better than three. Five is better than four, and so on.
Considering standard deviation in this example is 0.320 * 1.128 = 0.361 is the average range. Our spread of dispersion is ~ 0.361 units, yet our measure increments are less than that. Our measurement increments are in varying values of 0.01 which is less than our dispersion. It stands to reason that if we want to be able to detect variation, we need measurement increments that are less than standard deviation; else we cannot detect it. For example, if the only means for detecting the weights of humans is measured to the nearest ton, all humans would weigh zero tons.
“I Can’t Believe It’s Not Butter®”
It is a little-known fact that “I Can’t Believe It’s Not Butter®” suggests there is zero fat in their yellow spray bottle, when in fact there is fat in that bottle – and plenty of it.* The food producer is taking advantage of the FDA’s rules for rounding that measures grams of fat per serving down to the whole number. Since one squirt is the serving size (5 sprays for topping), and since five squirts is less than one half of a gram of fat, they round down to zero, and that is exactly what they put on the label.
*13 sprays is about 1 gram of fat, 25 sprays is about 2 grams of fat. 38 sprays is about 3 grams of fat. The whole bottle contains 90 grams of fat. So if you can’t believe it’s not butter, pour it on and watch the scale.
Why 6 units?
It has to do with the discrimination ratio. If you want more on this, read the book by Dr. Donald Wheeler, Evaluating the Measurement System, (2nd Ed.). Wheeler states,
“Since this problem [indiscriminate measurement] arises out of the inability to detect variation with the subgroups, the solution consists of increasing the ability to detect that variation. This can be done in one of two ways. Either use smaller measurement units, or increase the variation within the subgroups to a detectable level. The latter approach will usually be accomplished by collecting values for a subgroup over a longer time span. By increasing the time span, one often increases the variation enough to make it detectable with the original measurement units.”
It is referred to in the course as a larger inference space.